高楼翻译：软件压力测试中常用测试参数的估计方法

声明：本文若有侵权，请及时联系我，我会立即做删除处理。

• 原文出处：2011 International Conference on Computer Science and Network Technology
• 原文链接：http://barbie.uta.edu/~jxu/The estimation method of common testing parameters in software stress testing.pdf

原文名：《The Estimation Method of Common Testing Parameters in Software Stress Testing》
Meng Zhang, Honghui Li, Jun Xiao

• School of Computer and Information Technology
• Beijing Jiaotong University
• Engineering Research Center of Network Management Technology for High Speed Railway Ministry of Education Beijing, China
• 10120535@bjtu.edu.cn

译者注：
在性能行业中，并发用户数、并发峰值如何估算一直是争论的焦点。在之前我发过Eric的《Method for Estimating the Number of Concurrent Users》的译文，也说明了其中的问题点在哪里。
而在 2011 年的 International Conference on Computer Science and Network Technology，有一篇英文论文《The Estimation Method of Common Testing Parameters in Software Stress Testing》同样也是对这个关键问题进行论证的。
这是国人写的，但是在网上没有看到中文版。因为这是一篇会议论文，所以我也查了一下翻译论文是否侵权，也咨询了朋友。这样翻译带有原文链接、出处及作者信息，应该是不侵权的。
在文中，并发用户峰值不是用泊松分布近似到正态分布计算的，而是用切比雪夫不定式计算的。并且这一次的结果不是并发峰值C’=C+3x 根号C，让我们来看一下具体是什么样的过程。
在读本文之前，建议先读：《高楼翻译：并发用户数的估算方法（请仔细看译者注）》
因为本文和前文有着直接的关系，所以我想翻译一下，来看一看在性能的行业中，有哪些不同的声音。
在看的过程中请仔细思考，这个逻辑是否合理。

摘要：
在压力测试需求分析中，测试人员需要估计一些测试参数，这些参数用于设计不同应用程序的测试方案。这些测试参数始终会影响压力测试的准确性。本文在掌握随机过程和排队理论的基础上，对压力测试中常用的测试参数的估计方法进行了研究。通过在一些实际测试案例中的应用，我们验证了估计方法的有效性

一、引言

压力测试在系统测试阶段起着关键作用，压力测试是一种用于确定给定系统稳定性的测试形式，它涉及超出正常运行能力的测试[1]。压力测试显示了在更多用户同时访问数据的情况下系统的行为[2]。

在软件压力测试的需求分析阶段，测试人员需要从软件产品手册和用户调查中获取产品性能信息，并将其转换为由一系列测试参数描述的压力测试用例。尽管通用的自动化性能测试工具使并发模拟和性能监视的测试变得更加简单，但是它们不能帮助测试人员在压力测试的早期进行测试需求分析。在压力测试初期的测试需求分析中，测试人员需要估计不同应用程序的一些测试参数，例如并发访问次数，思考时间，并发增量变化等，这些测试参数始终会影响测试的准确性。压力测试。例如，在测试用例中，测量系统对需求的响应时间取决于当前寻求服务的用户数量。响应时间很长，但是对数据库服务器的存储有很大的影响[3]。为了帮助测试人员设计压力测试用例，提高压力测试的准确性，为优化软件性能提供可靠的测试结果，在掌握了随机过程和排队理论的基础上，我们对一些常用的测试参数进行了研究。在压力测试中，提出参数估计公式及其简单的推导过程。

二、估计当前用户数的方法

A.估计并发用户数的方法

为了进行规划和性能管理，有必要在测试和使用系统之前对并发用户数进行估算。通常，并发用户数直接影响系统资源。
不同的任务场景具有不同的并发用户数量，因此，在我们估计并发用户数量，分解任务之前，要关注业务运营的典型任务场景 ，然后，我们根据场景[4]使用一些方法来估计并发用户数。
首先，考虑如何计算并发用户数，即从任务角度合理设置多少并发量。当前，一种计算并发用户数的通用方法是假设该数量等于用户总数的一定百分比。该方法在某些测试方案中是有效的，但其准确性并不理想。现在介绍一种估计方法及其推导过程。
登录会话是从用户登录到用户退出之间的一段时间。在此期间，系统将创建一个用户会话，该用户会话消耗任何登录会话的系统资源，并且系统资源将使用一次或多次。因此，我们可以将t时刻的并发用户数定义为t时刻的登录会话总数。如果关注时间段T，则可以推导带有数学推导的公式（详细推导如 Eric Man Wong 的文章“估计并发用户数的方法” [5]（于2004年发表）：

如果在相关时间段T中有n个登录会话，并且每个登录会话的平均长度为L，则
（1）等效于：

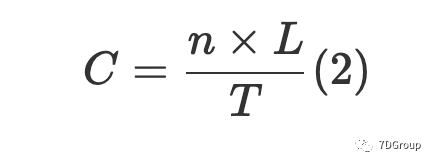
因此，得出了一个简单且可计算的公式，该公式大约是并发用户的平均数量。在该公式中，根据不同的应用场景，估算出相关时间段的长度T，关于登录会话数n是该关注时段内登录会话的数量，每个登录会话的平均长度L是该关注时段内登录会话总数的平均长度。以上三个参数可以在测试前通过需求分析获得。
有时，测试人员需要增加测试压力，这是系统可以执行压力测试的最大并发次数。接下来是最大并发数的讨论。
泊松概率分布广泛用于描述单位时间内独立随机事件的概率。在分析服务系统时，通常使用泊松概率分布来建立特定时间内用户到达数量的模型。这里假设单位时间内的登录会话数是具有参数/lambdaλ的泊松概率分布，则：

在此假设下，结合并发用户数的定义，可以证明单位时间内的并发用户数也是泊松概率分布。根据泊松概率分布的性质，泊松概率分布的参数 /lambdaλ 等于其数学期望值，也是平均值。已经获得平均并发用户数 C，然后可以给出单位时间内并发用户数的概率分布表达式：

这里的测试参数 C 可以通过公式（2）得到。和随机变量 X 表示公式（4）中每单位时间的并发用户数，则其期望值和方差分别为：

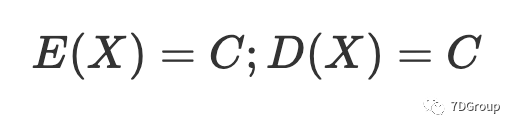
根据切比雪夫不等式[6]，对于任何正数都有不等式：

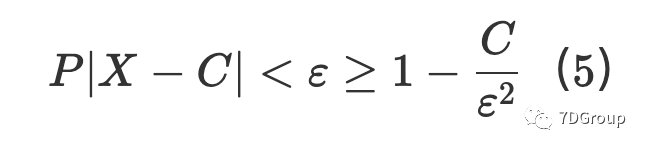
使用（5），它为我们提供了事件 P∣X−C∣<ε 采取概率的最小估计。假设 ε 是：

则：

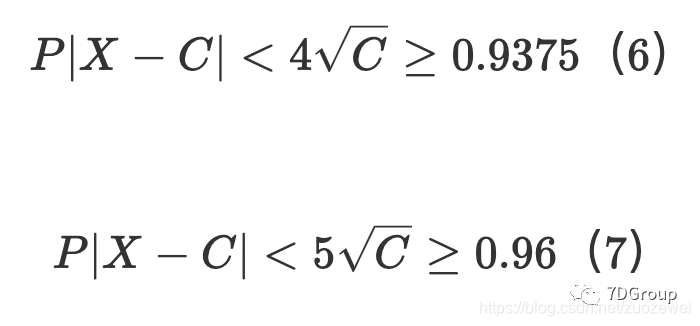
假设事件概率的下限接近1，则该事件的概率可以接近于1。因此，可以估计并发用户的峰值数量，我们可以用（6）和（7）获得并发用户的峰值数量。

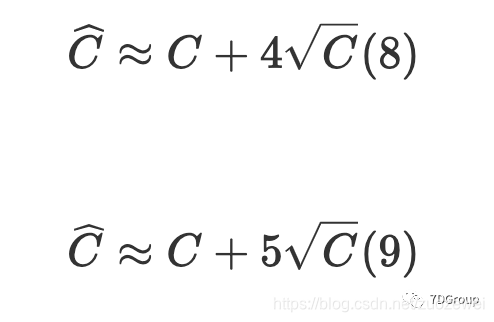
与 Eric Man Wong 的观察结果 [5] 相比，并发用户的峰值数量为

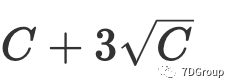
。我们的观察结果与他的观察结果不同。为了测试人员的计算目的，我们简化了公式，并提出了两个更适用的公式（8）和（9）来计算并发用户的峰值数量。

B.两种方法的分析

我们将讨论两种方法来估计并发用户数。
第一个是 Eric Man Wong 估算并发用户峰值数量的想法。Eric Man Wong 根据正态分布和 Poisson 分布之间的关系估计用户的峰值。首先，Eric Man Wong 假设每单位时间到达的用户数符合泊松分布，当总数超过 20 时，泊松分布近似于正态分布。在本文中，很明显，并发用户的平均数量远大于20。因此，具有 C 平均值的泊松分布近似视为正态分布，符合平均值为C和标准偏差为

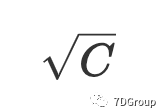
。假设并发用户数为X，则变量

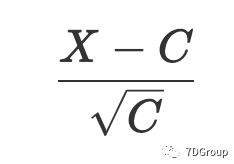
满足标准正态分布。可以从标准正态分布列表中获得以下方程式：

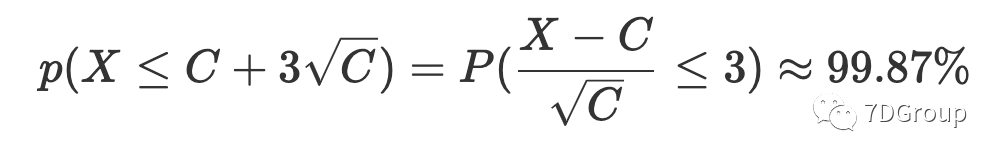
从上面我们可以得到的信息是并发用户数的概率较小比

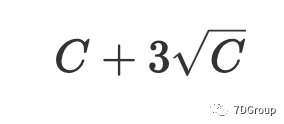
为 99.87％，且应用的可能性广泛且大。因此，根据 Eric Man Wong 的想法，我们可以计算出并发用户的峰值数量为

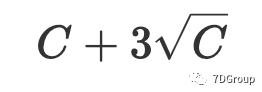
。与 Eric Man Wong 的想法相比，本文根据切比雪夫不等式的性质估计用户的峰值[6]。只要知道数学期望和方差，就可以获得有关随机变量分布的信息，因此切比雪夫不等式[6]的实用性很强。当 EX 和 DX 已经知道后，概率

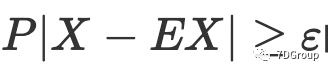
的上限可以根据切比雪夫不等式获得[6]，并且上限不涉及随机变量X的特定分布，而只涉及DX和ε。
针对本文的问题，概率

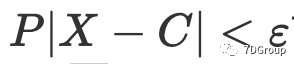
可以通过切比雪夫不等式获得，假设ε为

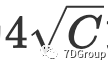
或

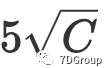
，那么我们可以得到并发用户数峰值为

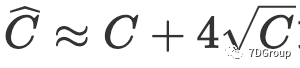
或

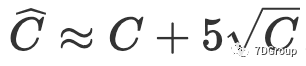
从上面我们可以通过比较两种估计并发用户峰值的方法得出结论：
1）

1. Eric Man Wong的想法是，在一定条件下，通过泊松分布与正态分布之间的近似关系来估计并发用户的峰值数量。即使参数λ的值大于20，泊松分布也近似视为正态分布，但仅当 λ 趋于 ∞ 时，泊松分布 X 趋于 π(λ) 等于正态分布。因此，就其本身而言，用 Eric Man Wong 的思想解决问题的过程是不准确的，并且不可避免地存在偏差。而且并发用户数是数值，因此用正态分布代替Poisson 分布不是理想的方法，因此结果并不理想。
2. 与 Eric Man Wong 的想法相比，我们通过切比雪夫不等式估计并发用户的峰值。如果我们使用切比雪夫不等式，则无需知道随机变量的具体分布，仅了解数学期望和方差就可以估计事件的上限和下限。根据我们的结果，

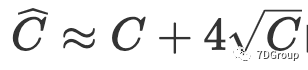
的概率为 93.75％，

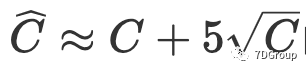
的概率为 96％，可见我们提出的可靠性很高。

三、估计吞吐量的方法

吞吐量是指“系统每单位时间要处理的请求数” [4]，直接反映了系统的处理能力。通常，吞吐量是通过请求/秒或页面浏览量来衡量的/秒。吞吐量与并发用户数之间存在一定的关系，当遇到性能瓶颈时，可以通过以下公式计算吞吐量：

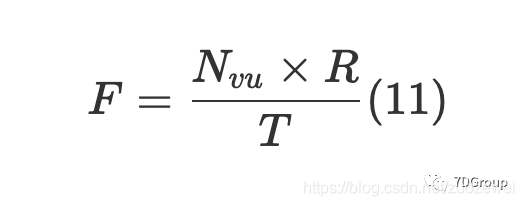
在这个公式中，F 是吞吐量，N_{vu} 表示虚拟用户数或并发用户数，R 表示每个用户的请求数，T 表示测试时间。但是当出现性能瓶颈时，吞吐量和并发用户数并不匹配。

四、用户思考时间的估算方法

思考时间，也称为“睡眠时间”，是用户从任务角度执行任务期间两个请求之间的时间间隔。当用户正在操作系统时，他们不太可能不间断地发起请求，更常见的模式应该是在用户发起请求之后，等待一段时间再发起另一个请求[4]。
设置思考时间是实际测试项目中的常见问题，那么如何设置它才是最合理的呢？实际上，思考时间，迭代次数，并发用户数和吞吐量之间存在一定的关系。假设每个用户的请求数是R，测试时间为T，用户的思考时间为T_s则：

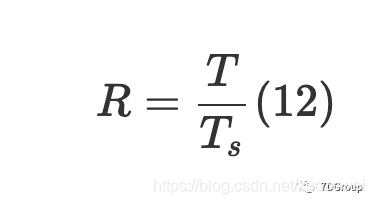
将公式（11）放在一起，我们可以获得有关思考时间的估计值：

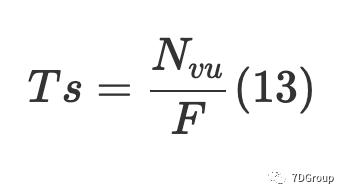
为了更准确地模拟测试场景，我们可以将公式（13）的估计值作为基准时间。实际思考时间在一定范围内随机浮动。
我们还需要引入“零思考时间”的思想，如果您将零用作思考时间，将会给系统带来更大的压力。从任务的角度来看，思考时间被用来更准确地模拟用户操作，因此，将参数设置为零没有真正意义。但是，如果您的目的是在巨大压力下测试其性能水平或了解其压力极限，则可以采用零思考时间。

五、增加用户到达量的估算方法

用户进行压力测试有两种方法。一种是用户同时到达，所有用户在测试开始时就可以访问系统并执行操作。另一种方法是逐渐增加加入用户的数量；用户访问系统的数量是一种递增的方法。尽管这两种方法生成的用户访问系统的次数相同，但是测试结果却不同。接下来讨论增量的估计方法。
假设用户的到达过程是一个泊松过程，平均到达率是λ，系统的服务率是一个固定值μ。该服务只有一个系统。通过用排队论中的M / G / 1 过程 [7] 分析过程，我们可以根据 P-K 均值公式（译者注：这里指的是 Pollaczek-Khintchine(P-K)公 式）得到平均响应时间：

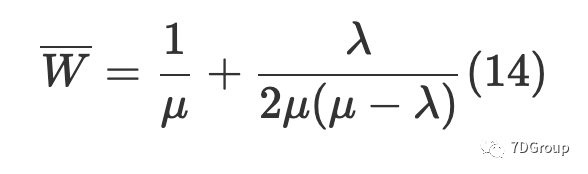
然后可以通过（14）获得平均到达率：

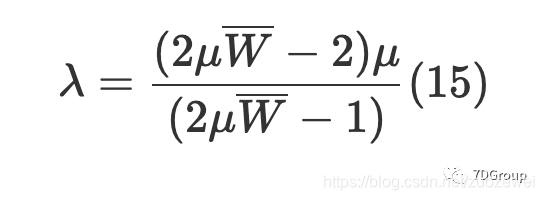
当系统处于稳定状态时，并发用户的平均增量可以由（15）估算，也就是平均到达率，在公式中，μ代表系统每单位时间要处理的请求数，以及

表示系统可以承受的平均响应时间。

六、测试应用

在上述压力试验中推导的几种常用试验参数的估算公式已应用于实际试验，取得了较好的效果。下面简单介绍一下压力测试估算公式的有关情况。
被测试的系统是“基于网格的铁路货运信息系统”。该系统主要用于查询和跟踪铁路基本数据，主要涉及三种类型的综合服务：货运组织和管理，货运收入的统计分析，货运营销。铁道部，铁路局和公众是主要用户。在对系统进行了UAT（用户接受测试）测试之后，在正式投入使用之前，需要对系统的性能进行测试并评估其可靠性，从而验证系统性能是否可以达到所需的并发用户数和响应时间。
通过分析系统的设计规范并调查用户，可以获得以下数据：
1）平均每天该系统的用户总数约为600。
2）用户的登录会话时间平均为4个小时，每天工作8个小时。
3）平均每个用户在登录会话时间内操作500个查询。
4）系统可以同时处理五个用户的请求。

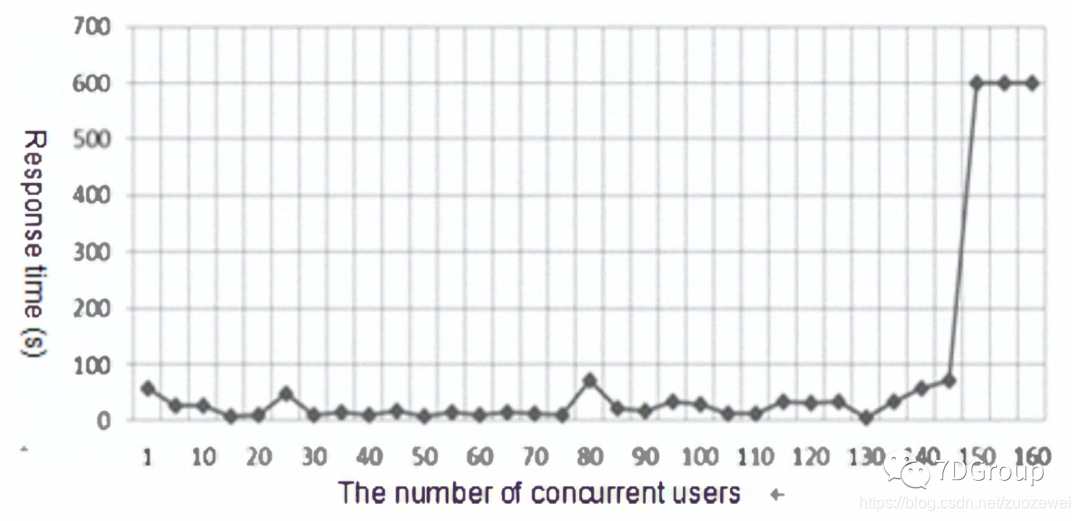
图1、并发用户数和响应时间关系图

5）用户可以忍受的平均响应时间少于10秒。

根据以前的估计方法，可以获得以下内容：

这些数据可用于设计以下测试案例设计中的下一个测试方案。
根据被测系统的分析，需要进行以下两个方面的压力测试：

1. 在平均并发用户数达到指标时, 系统的页面响应时间少于10秒；
2. 系统可以在并发用户数达到峰值的情况下，在48小时内连续稳定运行，即系统资源不会持续减少，用户响应率也不会发生明显变化。

下一步是配置测试环境，使用自动工具进行压力测试，进行压力测试和资源监控，从而获得测试结果。
测试了系统的 30 个功能页面，其中 21个功能页面的平均响应时间在 10 秒以内，其余均不能满足要求。当用户增加时，整个系统的平均响应时间的变化如图 1 所示。

七、结论

为了帮助测试人员分析压力测试需求并设计压力测试并发场景，提高压力测试的准确性，为软件的性能调整提供可靠的数据，本文在掌握随机过程和排队理论的基础上，研究了压力测试中常用的一些参数，并提出了一些软件压力测试中常用测试参数的估计方法。通过在一些实际测试案例中的应用，我们验证了估计方法的有效性。
本文从假设的泊松过程推导了基于用户到达系统的参数估计公式，并在其他随机过程模式的基础上推导了测试参数的估计公式。

致谢：
本文得到国家重大专项“交通基础软件在全国集成应用中的软件测试技术研究（2009ZX01045-005-001-03）”和北京交通大学985主题平台“高铁网络管理技术平台”的支持。

引用：

• [1] Guang.Yang, JianhuiJiang, Jipeng.Huang, “System modules interaction based stress testing model”.In: The Second International Conference on Computer Engineering and Applications, Bali Island, Indonesia, 19-21 March, 2010, pp. 138-141.(2010)
• [2] Motalova, L., Krejcar, 0., “Stress Testing Data Access via a Web Service for Determination of Adequate Server Hardware for Developed Software Solution”.In: The Second International Conference on Computer Engineering and Applications, Bali Island, Indonesia, 19-21 March, 2010, pp. 329-333.(2010)
• [3] Motalova, L., Krejcar, 0., “Stress Testing of User Adaptive Systems for Determination of Adequate Hardware Solution”. In: 9th RoEduNet IEEE International Conference, Sibiu, Romania, 24-26 June, 2010, pp.212- 217.(2010)
• [4] Nian.Duan., Software Performance Testing and Cases Analysis. Beijing : Tsinghua University Press,2006
• [5] Wong,E.M., Method for Estimating the Number of Concurrent Users[J]. Quality Techniques Newsletter (QTN). Software Research.2004.10
• [6] Zhou. Sheng, Shiqian. Xie, Chengyi. Pan, Probability Theory and Mathematical Statistics [M]. Beijing: Higher Education Press, 3rd Edition, 2001.
• [7] Rongheng. Sun, Jianping. Li, Fundamentals of Queuing Theory [M]. Beijing: Science Press, 2002

高楼注：

通读本文之后，请思考如下问题：

1. 关于到达率是否为泊松分布的问题，我在前文中已经有提到过了。关键是在落地时如何获得相应的到达分布。那问题就是，如果不是泊松分布，显然就没有E(X)=C和D(X)=C，这时怎么往下继续？
2. 在性能场景中，并发用户数的数学期望E(X)是否有不存在的可能？
3. 在第二部分直接使用了切比雪夫不等式进入了后续的计算，这里直接使用切比雪夫不等式有什么问题？
4. 切比雪夫定理中有描述：“任意一个数据集中，位于其平均数m个标准差范围内的比例（或部分）总是至少为1－1/m2，其中>m为大于1的任意正数”。根据此定理，如果并发用户数的平均值为100，那就是至少有99.99%的用户在100个标准差范围内。这>样的计算对性能场景中的并发用户数评估有什么实际的意义？
5. 在文中假设了ε是“4x根号C”或“5x根号C”，这个假设有什么问题吗？
6. 文中用测试时间T/Ts来计算请求数，这个请求数在具体的技术角度指的是什么？这个计算方法有什么问题？
7. 文中用公式11、12获得的思考时间估计值公式13，有什么价值？
8. 在第五部分中，这里用到了排队论M/G/1过程，后面使用了P-K公式代入计算，这个过程有什么局限？是否具有通用性？
9. 接上一问题，如果不是M/G/1过程的系统，又应该如何处理？
10. 接上一问题，是否要计算M/G/1过程的稳态概率？
11. 在一个真实的系统中，通常会是多个子系统组成的业务链路，这时应该用什么样的模型来计算？