1828. 统计一个圆中点的数目：

给你一个数组 points ，其中 points[i] = [
$x_i$,
$y_i$] ，表示第 i 个点在二维平面上的坐标。多个点可能会有 相同 的坐标。

同时给你一个数组 queries ，其中 queries[j] = [
$x_j$,
$y_j$,
$r_j$] ，表示一个圆心在 (
$x_j$,
$y_j$) 且半径为
$r_j$ 的圆。

对于每一个查询 queries[j] ，计算在第 j 个圆 内 点的数目。如果一个点在圆的 边界上 ，我们同样认为它在圆 内 。

请你返回一个数组 answer ，其中 answer[j]是第 j 个查询的答案。

样例 1

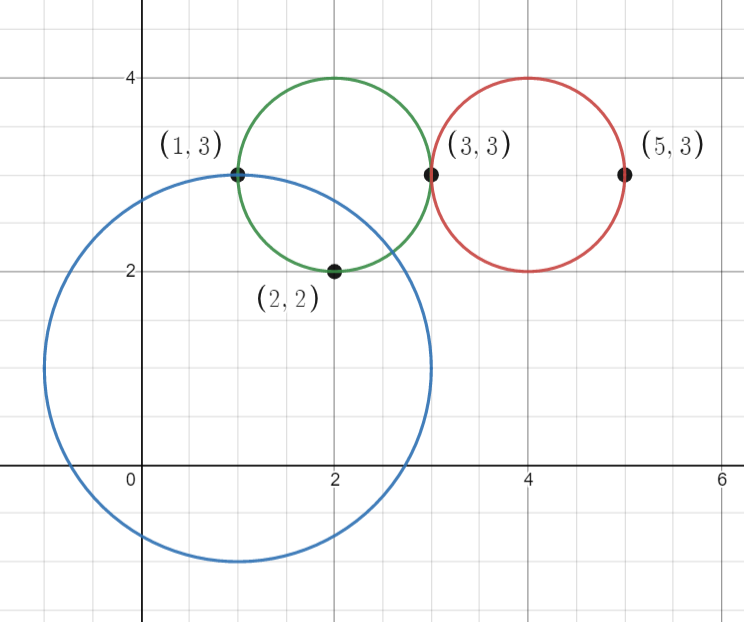
输入：
	points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
    
输出：
	[3,2,2]
    
解释：
	所有的点和圆如上图所示。
	queries[0] 是绿色的圆，queries[1] 是红色的圆，queries[2] 是蓝色的圆。

样例 2

输入：
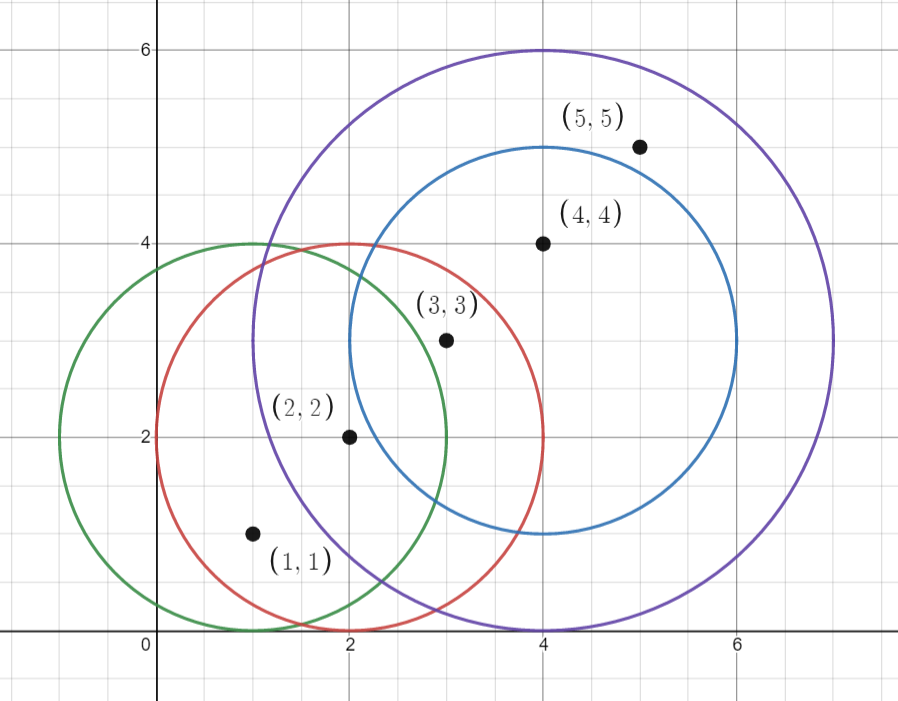
	points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
    
输出：
	[2,3,2,4]
    
解释：
	所有的点和圆如上图所示。
	queries[0] 是绿色的圆，queries[1] 是红色的圆，queries[2] 是蓝色的圆，queries[3] 是紫色的圆。

提示

• 1 <= points.length <= 500
• points[i].length == 2
• 0 <=
  $x_i$,
  $y_i$ <= 500
• 1 <= queries.length <= 500
• queries[j].length == 3
• 0 <=
  $x_j$,
  $y_j$ <= 500
• 1 <=
  $r_j$ <= 500
• 所有的坐标都是整数。

分析

• 二当家的刚看到题目先是有点懈怠心里，因为几何知识都忘记了，感觉会很复杂。
• 但是读了题，仔细思考后发现点是否会落在圆内，就是要看点到圆心的距离是否小于等于圆的半径。
• 假设圆心
  $p_1$ 的坐标是（
  $x_1$，
  $y_1$），点
  $p_2$ 的坐标是（
  $x_2$，
  $y_2$），那么点到圆心的距离就是
  $/sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}$。
• 由于我们只需要比较距离和半径哪个大，并不需要真的算出距离，所以可以距离不开方，而把半径做平方，因为平方运算要比开方快。

题解

java

class Solution {
    public int[] countPoints(int[][] points, int[][] queries) {
        final int n   = queries.length;
        int[]     ans = new int[n];

        for (int i = 0; i < n; ++i) {
            int x = queries[i][0];
            int y = queries[i][1];
            int r = queries[i][2];
            int r2 = r * r;
            int maxX = x + r;
            int minX = x - r;
            int maxY = y + r;
            int minY = y - r;

            for (int[] p : points) {
                int px = p[0];
                int py = p[1];
                // 加速的判断，是否有意义不好说，对于不符合的点会更快，对于符合的点会更慢，也许就互相抵消了
                if (px < minX || px > maxX
                    || py < minY || py > maxY) {
                    continue;
                }
                // 到圆心距离小于等于半径的点就是满足题目要求的点
                double dis = Math.pow(px - x, 2) + Math.pow(py - y, 2);
                if (dis <= r2) {
                    ans[i]++;
                }
            }
        }

        return ans;
    }
}

c

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* countPoints(int** points, int pointsSize, int* pointsColSize, int** queries, int queriesSize, int* queriesColSize, int* returnSize){
    *returnSize = queriesSize;
    int *ans = malloc(sizeof(int) * queriesSize);

    for (int i = 0; i < queriesSize; ++i) {
        int x = queries[i][0];
        int y = queries[i][1];
        int r = queries[i][2];
        int r2 = r * r;
        int maxX = x + r;
        int minX = x - r;
        int maxY = y + r;
        int minY = y - r;

        int count = 0;

        for (int j = 0; j < pointsSize; ++j) {
            int px = points[j][0];
            int py = points[j][1];
            // 加速的判断，是否有意义不好说，对于不符合的点会更快，对于符合的点会更慢，也许就互相抵消了
            if (px < minX || px > maxX
                || py < minY || py > maxY) {
                continue;
            }
            // 到圆心距离小于等于半径的点就是满足题目要求的点
            double dis = (px - x) * (px - x) + (py - y) * (py - y);
            if (dis <= r2) {
                ++count;
            }
        }

        ans[i] = count;
    }

    return ans;
}

c++

class Solution {
public:
    vector<int> countPoints(vector<vector<int>>& points, vector<vector<int>>& queries) {
        vector<int> ans;

        for (auto &query : queries) {
            int x = query[0];
            int y = query[1];
            int r = query[2];
            int r2 = r * r;
            int maxX = x + r;
            int minX = x - r;
            int maxY = y + r;
            int minY = y - r;

            int count = 0;

            for (auto &point : points) {
                int px = point[0];
                int py = point[1];
                // 加速的判断，是否有意义不好说，对于不符合的点会更快，对于符合的点会更慢，也许就互相抵消了
                if (px < minX || px > maxX
                    || py < minY || py > maxY) {
                    continue;
                }
                // 到圆心距离小于等于半径的点就是满足题目要求的点
                double dis = (px - x) * (px - x) + (py - y) * (py - y);
                if (dis <= r2) {
                    ++count;
                }
            }

            ans.push_back(count);
        }

        return ans;
    }
};

python

class Solution:
    def countPoints(self, points: List[List[int]], queries: List[List[int]]) -> List[int]:
        ans = []

        for x, y, r in queries:
            r2 = r * r
            maxX = x + r
            minX = x - r
            maxY = y + r
            minY = y - r

            count = 0
            for px, py in points:
	            # 加速的判断，是否有意义不好说，对于不符合的点会更快，对于符合的点会更慢，也许就互相抵消了
                if (px < minX or px > maxX
                        or py < minY or py > maxY):
                    continue
                # 到圆心距离小于等于半径的点就是满足题目要求的点
                dis = (px - x) ** 2 + (py - y) ** 2
                if dis <= r2:
                    count += 1

            ans.append(count)

        return ans

go

func countPoints(points [][]int, queries [][]int) []int {
    ans := make([]int, len(queries))

	for i, query := range queries {
		x := query[0]
		y := query[1]
		r := query[2]
		r2 := r * r
		maxX := x + r
		minX := x - r
		maxY := y + r
		minY := y - r

		for _, point := range points {
			px := point[0]
			py := point[1]
			// 加速的判断，是否有意义不好说，对于不符合的点会更快，对于符合的点会更慢，也许就互相抵消了
			if px < minX || px > maxX || py < minY || py > maxY {
				continue
			}
			// 到圆心距离小于等于半径的点就是满足题目要求的点
			dis := (px - x) * (px - x) + (py - y) * (py - y)
			if dis <= r2 {
				ans[i]++
			}
		}
	}

	return ans
}

rust

impl Solution {
    pub fn count_points(points: Vec<Vec<i32>>, queries: Vec<Vec<i32>>) -> Vec<i32> {
        queries.iter().map(|query| {
            let (x, y, r) = (query[0], query[1], query[2]);
            let r2 = r * r;
            let max_x = x + r;
            let min_x = x - r;
            let max_y = y + r;
            let min_y = y - r;

            points.iter().map(|point| {
                let (px, py) = (point[0], point[1]);
                if px >= min_x && px <= max_x
                    && py >= min_y && py <= max_y {
                    // 到圆心距离小于等于半径的点就是满足题目要求的点
                    let dis = (px - x) * (px - x) + (py - y) * (py - y);
                    if dis <= r2 {
                        return 1;
                    }
                }
                0
            }).sum()
        }).collect()
    }
}

原题传送门：https://leetcode-cn.com/problems/queries-on-number-of-points-inside-a-circle/

非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】~
放弃不难，但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子：https://bbs.huaweicloud.com/community/usersnew/id_1628396583336561 博客原创~